1 Introduction

Deep reinforcement learning (RL) has proven to be very successful in many challenging tasks. [33, 48, 8]. These were considered intractable just a few years ago. However, current methods require enormous amounts of compute to achieve great performance in individual tasks. This compute just goes to waste very often when new tasks are considered, even if the environment does not change. Not long ago this was also the case in Computer Vision and Natural Language Processing, until unsupervised learning took off. By using task agnostic pre-training schemes, generalist models have revolutionized both fields [14, 53, 10]. They can solve most tasks with minimal or even no fine-tuning, Unsupervised Reinforcement Learning aims to bring similar successes to the Reinforcement Learning community. By discovering a wide range of skills that cover diverse behaviours in an environment, we will be able to solve new tasks, beyond what could be imagined when the model was trained, with minimal or even no training.

Here, we propose a new method for open-ended, unsupervised skill discovery. We devise an iterative process which creates pairs of neural reward functions together with policies that can solve the corresponding reward function. Each policy corresponds to a skill that the agent has learnt. The neural reward function is a neural network that maps the current observation to a scalar reward. In each iteration, the neural reward function is modified to differ from the previous one. This results in increasing the complexity of the encoded task. Then, a new skill is learnt that optimizes this reward function. We devise several techniques to transfer the knowledge from previously learnt skills. These mechanisms enable learning of the most complex reward functions that our method creates. In fact, we show that some of the functions are impossible to learn from scratch.

We empirically test our framework in a diverse set of environments. First, we apply it to a simple 2d navigation task. This lets us perform experiments quickly and gain a solid empirical understanding of the different components of our method. Then, we apply it to three robotic environments where we have continuous high-dimensional observations and actions. Finally, we apply it on the challenging Montezuma’s Revenge Atari game which has visually rich pixel based observations and discrete actions. Despite their differences, our method manages to learn useful and interesting skills in all of them. This shows that neural reward functions are equipped to encode meaningful tasks in very diverse environments. We highlight the most important findings of this paper:

• Solve a 2d maze that cannot be solved by using random exploration.
• Learn to run as fast in Humanoid as a supervised RL agent trained for tens of millions of steps.
• Achieve a higher Particle-Based Mutual Information Metric [28] than approaches that use expert knowledge for feature engineering.
• Collect the first key and reach several rooms in Montezuma’s Revenge.

2 Related Work

Our work fits best into the unsupervised skill discovery literature [35, 27, 20, 2, 19, 46, 15]. Compared to DIAYN [19] and similar approaches, we do not set the number of skills to be learnt at the beginning of training. This allows us to learn new skills in an open-ended fashion. On top of that, maximizing mutual information can lead to degenerate behaviours in high-dimensional environments. By manipulating a small subset of the dimensions, a lot of information can be encoded, without exploring the rest of the state space.

Open-ended learning [56, 13, 16, 57, 18, 51] is closely related to unsupervised skill discovery. However, most approaches require either a parameterizable environment [56, 57], some fixed encoding of tasks [51] or self-competition [47, 5]. This limits the applicability to environments that are engineered with these restrictions in mind. In contrast, neural networks are universal function approximators and thus, our approach can encode any possible task in any possible environment, as long as the input is chosen appropriately.

Another related line of research to our approach is intrinsic motivation. [50, 6, 38, 12, 11, 42]. These approaches have managed great success in hard-exploration Atari games. However, these approaches do not learn discrete skills that can be composed or fine-tuned for fast learning of new tasks. This has limited their applicability to robotic environments where exploration is not usually the limiting factor.

There has been previous work using neural networks to output reward to RL agents. Compared to our work, they use supervision to train the reward function. Many of them train a reward function trained with states/trajectories labeled by supervisors in some fashion [1, 25, 49, 31]. Other approaches train auxiliary rewards with meta-learning [60, 17, 55] to enhance the learning of the original reward function.

Another approach to train multiple behaviours is goal-conditioned learning [29, 44, 4, 43, 36, 54, 58, 39, 15]. In automated curriculum learning [7, 21, 23, 26, 52, 22, 32, 37, 40, 41, 59], a sequence of goals is created such that each of them is not too hard nor too easy for the current agent. These approaches mostly rely on low-dimensional goal embeddings. When dealing with high-dimensional observations, they must use dimensionality reduction techniques. These techniques can introduce instabilities or destroy relevant information from the input. Our approach, on the other hand, can deal with high-dimensional inputs directly. On top of that, goals encode a narrow region of the state space, while each of our reward functions can be rewarding in a large region. This speeds-up the exploration in ’easy’ regions of the state space.

3 Method

We introduce a method that performs open-ended, unsupervised skill discovery. It iteratively creates pairs of neural reward functions $R_{\psi }$ and policies ${\pi }_{𝜃}$ trained to maximize the corresponding $R_{\psi }$. Our proposed method alternates between increasing the complexity of the reward function $R_{\psi }$ and leveraging the previously learnt skills to learn a policy ${\pi }_{𝜃}$ that can solve the new $R_{\psi }$. This yields a general learning procedure that learns complex skills in a diverse set of environments. See Figure 2 for a high level overview.

3.1 Increasing the complexity of $R_{\psi }$

The reward function in a fully observable Markov Decision Process (MDP) is by definition a function of the current observation, the next one and the action that was performed. However, in many cases this can be reduced to a function of just the current observation and because of this, we opt for these simpler reward functions as the basis of our $R_{\psi }$. In our method, the reward function $R_{\psi }$ is a neural network which takes observations $o_t$ as input and outputs a single scalar value, the instantaneous reward $r_t^{\psi }$.

Assume that we already have a policy ${\pi }_{𝜃}$ that can reach states in the MDP which are rewarding under $R_{\psi }$. To increase the complexity of the reward function, we want to do the following:

• Decrease the reward of states which are visited by ${\pi }_{𝜃}$, as we already have a policy that can reach these states. We will create a dataset $O_{neg}$ of such states, which we will refer to as negative samples.
• Increase the reward of states that can almost be reached by the current policy. This will allow us to leverage ${\pi }_{𝜃}$ to learn the new reward function. We will create a dataset $O_{pos}$ of such states, which we will refer to as positive samples.

To generate the negative samples, we run ${\pi }_{𝜃}$ for a given number of steps (ideally until it reaches rewarding states) and store the visited states. To then generate positive samples, we change to performing random actions ¹ for a fixed number of steps. To ensure that the new reward function is different from all previous ones, we also keep track of all the negative samples that we have collected for all skills in a dataset $O_{neg\text{\_}all}$.

Finally, we set target values $a$ and $-a$ for the positive and negative samples respectively, and train the reward network using standard supervised learning on the following loss:

This loss ensures that positive samples that have never been seen before, will have positive reward in the next $R_{\psi }$, while all other samples that have been seen before will decrease their reward. In the Reinforcement Learning phase we clip rewards to the $\left[0,a\right]$ range. This ensures that the agent seeks only positive samples, rather than less negative ones.

3.2 Forward transfer for ${\pi }_{𝜃}$

Given the procedure presented in Section 3.1, we create increasingly complex reward functions. While this is great for open-ended learning, it eventually leads to skills that are too complex and cannot be learnt from scratch. In order to learn these skills, we must leverage previous knowledge about the environment. In this section we present several forward transfer mechanisms that are necessary for the most complex skills.

Our method so far can be combined with any standard Reinforcement Learning (RL) technique but we will focus on Actor-Critic methods like Advantage Actor-Critic [34] or Proximal Policy Optimization [45] for learning ${\pi }_{𝜃}$. These methods have a value network that’s separate from the policy one which will allow us to transfer the most knowledge from the previous agent. Also, these approaches work both for continuous and discrete action spaces, allowing us to use the same technique for robotic environments or for 2d navigation tasks. Finally the learnt policies are stochastic, which increases the diversity of negative samples and speeds up the skill discovery process. See Section 4.1.2.

We present our three forward transfer mechanisms below. They all exploit the similarity between consecutive reward functions to ensure that even very complex reward functions can be solved by the RL agent in a reasonable amount of environment interactions.

• Value Reuse: Initialize the value network to the final value network of the previous agent. While two consecutive reward functions are different, both still reward close-by regions of the state space. Thus, by keeping the previous value function, the policy network will be nudged towards that region of the state space from the very first gradient updates.
• Policy Feature Reuse: Initialize the policy network to the final policy of the previous agent but setting the weights of the final layer to $0$. This keeps the features learnt before, but outputs a uniform policy over all actions (or mean $0$ and a fixed standard deviation in the continuous case), which allows for proper learning and exploration ² .
• Guiding Policy: Act with the previous policy for a random number of steps at the beginning of each episode. This heavily simplifies the exploration problem. The agent will start exploring from states that are much closer to the rewards defined by $R_{\psi }$. This is because the previous policy could already solve the previous reward function. In contrast to the other two mechanisms, this one does not rely on initialization. This means that it is the most effective in very sparse reward functions that will need many parameter updates to be learnt.

In Section 4.1.1 we individually evaluate these three techniques and show that their combination is necessary in complex environments.

Putting everything together we get an algorithm that can both, learn reward functions that encode increasingly complex behaviours and learn RL agents that solve those reward functions. Figure 2 illustrates the main steps of our training loop and Algorithm 1 shows the steps in more detail.

4 Experiments

We now proceed to experimentally test our method. First, in Section 4.1, we thoroughly test all different components of our model in a 2d navigation task. This task allows us to verify the function of each component and also to explicitly visualize what each reward function is encoding.

Then, in Section 4.2, we move to BRAX robotic environments [24]. These have the most flexibility and thus allow the agent to learn very complex tasks. In these tasks, we evaluate the complexity of our skills by measuring their zero-shot transfer ability to the environment rewards. In the Humanoid environment, our unsupervised skills outperform supervised agents trained for tens of millions of time steps. We also compute the one dimensional particle-based mutual information metric that has been proposed in the literature before [28] and show that our method outperforms previous approaches, even when other approaches only consider handcrafted feature dimensions in their objective.

Finally, in Section 4.3, we apply our method to Montezuma’s Revenge. We show that the learnt reward functions keep getting increasingly complex and we are mostly limited by the amount of compute that it takes to learn each new reward function.

4.1 2D Navigation Task

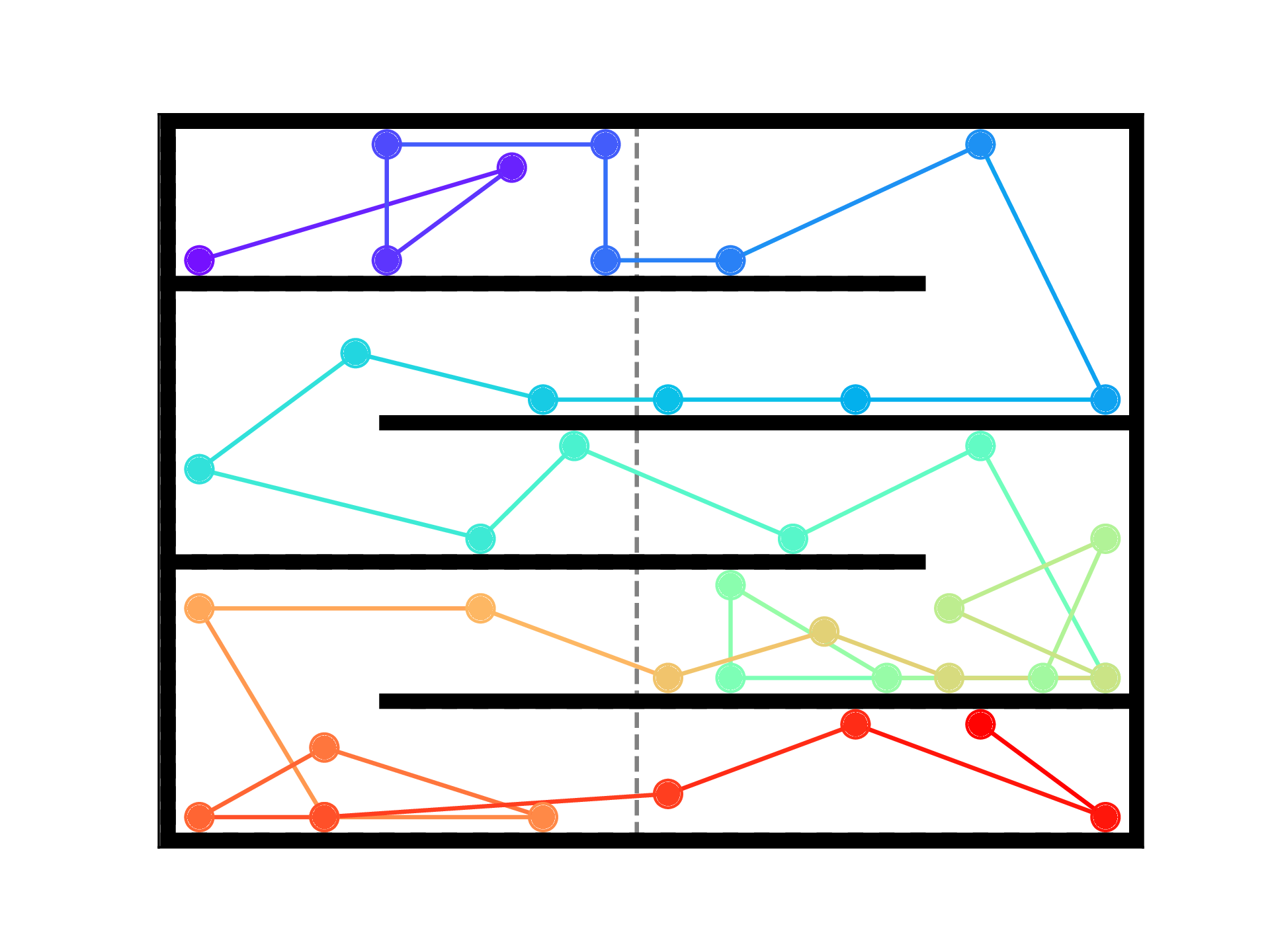
The task consists of a 32 by 32 maze with several walls and a ”danger zone”. The observation is given as a $32$x$32$x$1$ image with all values set to $0$, except a $1$ in the current position of the agent. The agent always starts in the top left corner and can always perform $5$ actions, either move in one of the cardinal directions or stay in the current position. If the agent moves into a wall it will stay at its current position instead. If the agent is in the ”danger zone” and moves up, moves down or stays, the episode is terminated and the agent is moved back to the starting position. Figure 3 shows the layout of the maze. The ”danger zone” ensures that random exploration will not work to reach many parts of the environment and lets us easily test both the increasing complexity of the reward functions and the importance of forward transfer. We computed the expected number of steps to reach the bottom right corner with a random walk using Dynamic Programming. In expectation, $7\cdot 10^{27}$ episodes are needed to do so. This shows that this maze is diffcult to navigate.

To train our agent we use the Advantage Actor Critic (A2C) [34] algorithm. To learn the rewards we use the full algorithm presented in Section 3. We use the same architecture for the reward, policy and value networks, but do not share any parameters. The architecture is a ReLU network with 2 convolutional layers followed by 2 fully connected layers. Figure 3 plots the most visited locations for each skill of one run of our algorithm. The first few skills visit points near the origin, later skills start moving to harder to reach parts of the state space. After roughly $40$ iterations they reach the bottom right part. As stated before, this would take unreasonably long when using only random exploration.

Inspired by the BRAX library [24], we implemented both the environment and an A2C agent inside a single JAX [9] compiled function. By doing this, the computation graph of the environment and agent are optimized jointly and both run on the GPU. This eliminates the need to send data between the CPU and GPU, which is one of the main bottlenecks in RL. Using just one NVIDIA RTX 3090 GPU, the training process runs at over one million frames per second, which enables training of agents in just a few seconds. This allows us to experiment quickly and at a very low economic and environmental cost. We believe this code is useful for the RL community on its own and we will make it available upon publication.

4.1.1 Forward transfer of skills

As pointed out in Section 3.2, our reward functions become too complex to be learned from scratch with random exploration in a reasonable number of steps. When this happens, our agent must rely on transferring knowledge from previous generations. Our navigation task is specifically designed to test this transfer ability, as random exploration would never reach the bottom right corner ($7\cdot 10^{27}$ episodes in expectation).

We experimentally evaluate the three forward transfer mechanisms proposed in Section 3.2: Value reuse, Policy feature reuse and Guiding policy. The reward functions from Figure 3 serve as tasks, sorted according to creation order. We train ablations of the three mechanisms sequentially on these tasks. This allows us to ignore the skill discovery process and only measure the forward transfer of skills. We repeat each experiment three times. The agent with all mechanisms, always manages to solve ³ all reward functions. On the other hand, the Policy, Value and Guiding ablations fail to learn after solving $29.3\pm 9.5$, $18.7\pm 11.6$ and $19\pm 8.5$ reward functions, respectively.

4.1.2 Speeding-up deep exploration

One key parameter when training actor critic methods is entropy regularization. In our method, policies with a lot of entropy will generate a diverse set of negative samples. Diverse negative samples lead to reward functions that evolve more in each generation. This is especially beneficial in environments where many steps are necessary to reach certain states, like in this 2D navigation task or Montezuma’s Revenge. We empirically verify this claim by training a set of agents with varying levels of entropy regularization. Figure 4 shows the coverage of the state space after $40$ generations as a function of the entropy regularization. It can be seen that higher entropy leads to a faster coverage of the state space up to a certain threshold. However, too much entropy leads to poor policies that do not learn to reach the rewarding states when these are far enough from the origin. Observe that this problem arises independent of the training procedure as the entropy regularization changes what the optimal policy is.

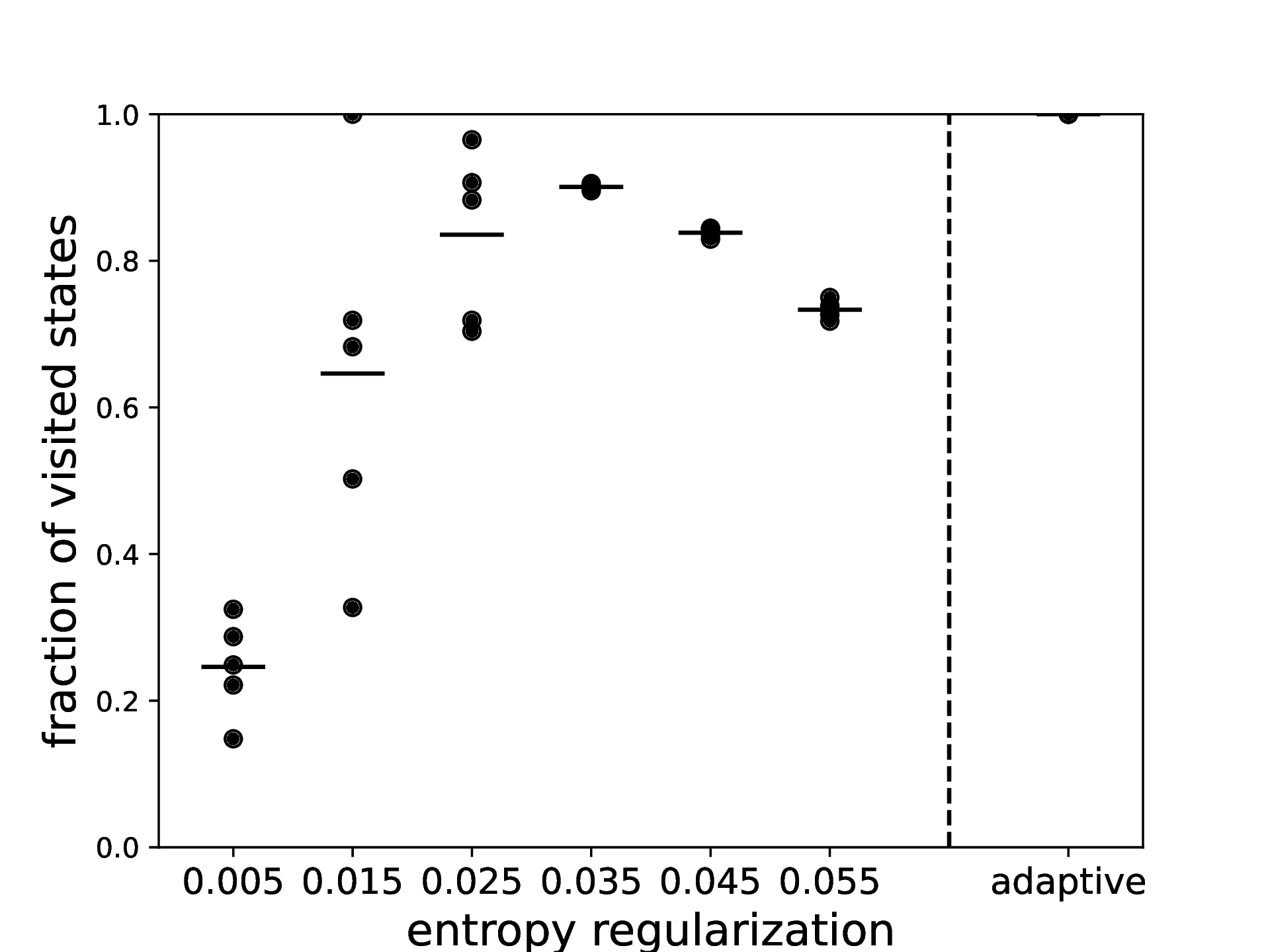
In order to have policies that gather diverse samples to change the reward function and that can also be deterministic in dangerous parts of the trajectory that already have no reward, we use adaptive entropy regularization. That is, we apply a small entropy regularization term everywhere. We increase the entropy regularization in states where the reward function is positive (states in which we want to decrease the reward function). By doing this, we manage to consistently visit all states in the maze. This technique was necessary to create the reward functions from Figure 3.

4.2 Robotic Environments

Quantitatively measuring Unsupervised Reinforcement Learning progress remains an open problem and active area of research. Because of this, it is still important to visualize and qualitatively study the learned skills. We do this in Section 4.2.1. In the next two Sections, 4.2.2 and 4.2.3, we quantitatively measure the performance of our algorithm on downstream task performance and with the so-called particle-based mutual information metric, respectively.

In contrast to the previous experiments, the action space is continuous and the input modality is now a vector of features, like relative position, angle and speed of the different joints. We do not use adaptive entropy here, as we need deterministic policies to maximize the downstream task performance and the mutual information metric. Given that the environments do not have far away regions to reach, we did not implement the guiding algorithm here. Note that the agent does not see the $x$-$y$ position.

4.2.1 Qualitative Analysis

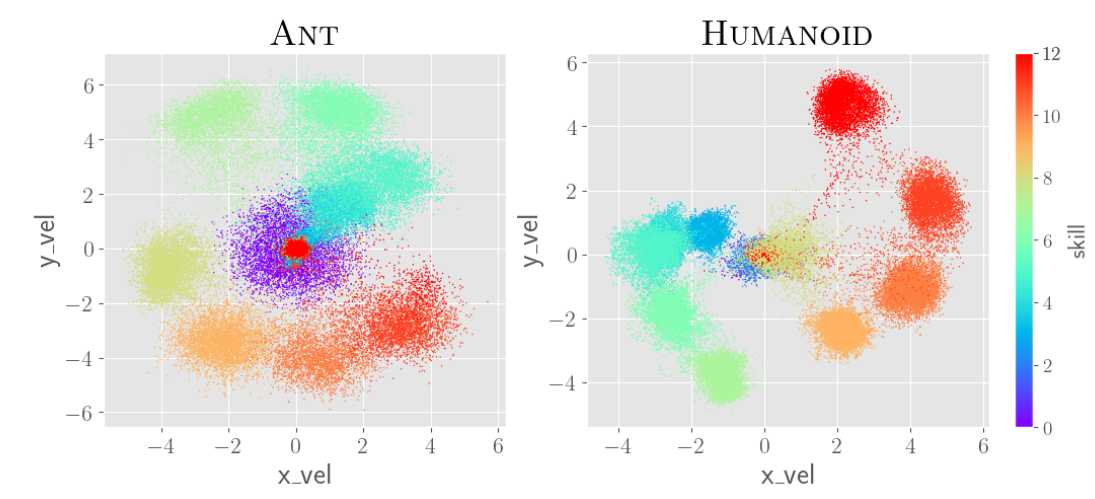
In Figure 5 we illustrate a selection of particularly interesting skills. In Figure 7 we see how the velocity of learnt skills in Ant and Humanoid evolve over training. In Figure 6 we visualize several consecutive skills. One can see that consecutive skills slightly change the direction and speed of moving. However, it is important to realize that the observations contain tens to hundreds of dimensions and thus, the skills can encode much more complex behaviors than speed/direction of movement. For example, Figure 5 shows that the skill involves keeping one leg in the air on top of moving in the right angle/speed.

4.2.2 Zero-Shot Transfer

After discovering $50$ unsupervised skills, we identify the skill that aligns best with the reward given by the environment. We report this zero-shot ⁴ performance in Table 1. As a baseline, we train an agent from scratch and measure how long it takes it to reach an equivalent performance. We use the Optuna hyperparameter optimizer [3] to find hyperparameters which maximize the speed of learning beforehand.

The simplest environment, Half-Cheetah , benefits the least from unsupervised learning, while the hardest one, Humanoid, benefits the most. This is in line with what is observed in Computer Vision and Natural Language Processing, of more complex tasks benefiting the most from a longer pre-training phase.

4.2.3 Particle-based Mutual Information metric

Measuring how well the agent can control relevant state dimensions is another way to track progress in Unsupervised Reinforcement Learning. This is measured using the mutual information between state dimensions and skills. While high-dimensional estimation of mutual information an active area of research, sampling can be an effective form of estimation in the 1-dimensional case, c.f. Algorithm 1 in [28]. We report the particle-based mutual information for the $x$-velocity in Table 2, using the same bucketing strategy ⁵ as in [28].

Our method far outperforms DIAYN, when both methods look at the whole observation state. DIAYN achieves diversity by learning a set of skills that can be correctly labeled by a neural network. In high-dimensional spaces this is easy to do by relying on a small subset of all state dimensions. This leads to non-diverse behaviours across most state dimensions. Even when expert knowledge about relevant dimensions is supplied to other methods, i.e. only taking the $x$- and $y$-velocity into account, our method still fares well. Particularly, in the most complex environment, Humanoid, our method comes on top. We believe the fact that our method does not partition the space, leads to a narrower coverage of the state space per skill (see Figure 7). Also the iterative increase in complexity leads to better coverage of hard to reach regions of the state, e.g. high velocity. With all this, our approach achieves greater controllability of the $x$-velocity without any kind of feature engineering.

4.3 Montezuma’s Revenge

To show the generality of our approach we evaluate it on the notoriously hard Montezuma’s Revenge Atari game. In this game, the agent controls a character in a complex 2d world with several rooms. Same as in [33], the observation is a stack of the last $4$ frames. This gives the agent information about speed and direction of movement. This is done for all networks, that is, the value, policy and neural reward networks. We use the same simple CNN architecture as in [33] for all three networks.

Our algorithm uses finite episode lengths because once it reaches a rewarding state, the agent can stay there forever. Because of this, we reset the environment every $500$ steps.

One of the main diffculties when dealing with Montezuma’s Revenge is that it cannot be simulated as fast as the other studied environments. On top of that, an agent can learn hundreds of different skills without ever leaving the first room. Finally, skills learnt by our agent evolve from simple to very complex and extended in time. In the beginning, the agent just needs to stay close to the initial position. By the end of training, the agent learns to collect a key, open the door and visit distant rooms. In the most complex skills, it takes the agent several hundred steps to reach a rewarding state. This means that experiments can take several days to visit a different room.

In order to save computation, we adapt the number of training steps according to several criteria. This lets us save a lot of compute on the skills which are easy to learn. We use the following measures:

• We train for $1M$ steps with guiding from the previous policy. The number of guiding steps is sampled uniformly at random between $0$ and $450$, each time the environment is reset. Then we train for another $0.65M$ steps without any guiding.
• If the average reward goes down after removing the guiding or is too low at any point, we restart the guiding phase for $0.65M$ steps.
• If the agent is reaching a terminal state in more than $10\%$ of the episodes, we continue training.

On top of this, we ignore positive samples that receive almost no reward. All these tricks enable us to considerably reduce the training time. However, they are not a core change in our algorithm as they could all be replaced by just training all generations for a longer fixed number of steps, just as before.

We found out that the first thing the agent learns is to get the life counter to $0$. Then it starts exploring the room, with $0$ lives already. This is because losing a life happens very easily during random exploration and because once the agent reaches $0$ lives, all future positive samples will have $0$ lives. This has two side effects. On the one hand, the initial $100-200$ steps of an episode are spent losing lives. On the other hand, exploration is harder, as the agent will reach a terminal state very easily. Because of this, we cut out the part of the image that shows the remaining lives.

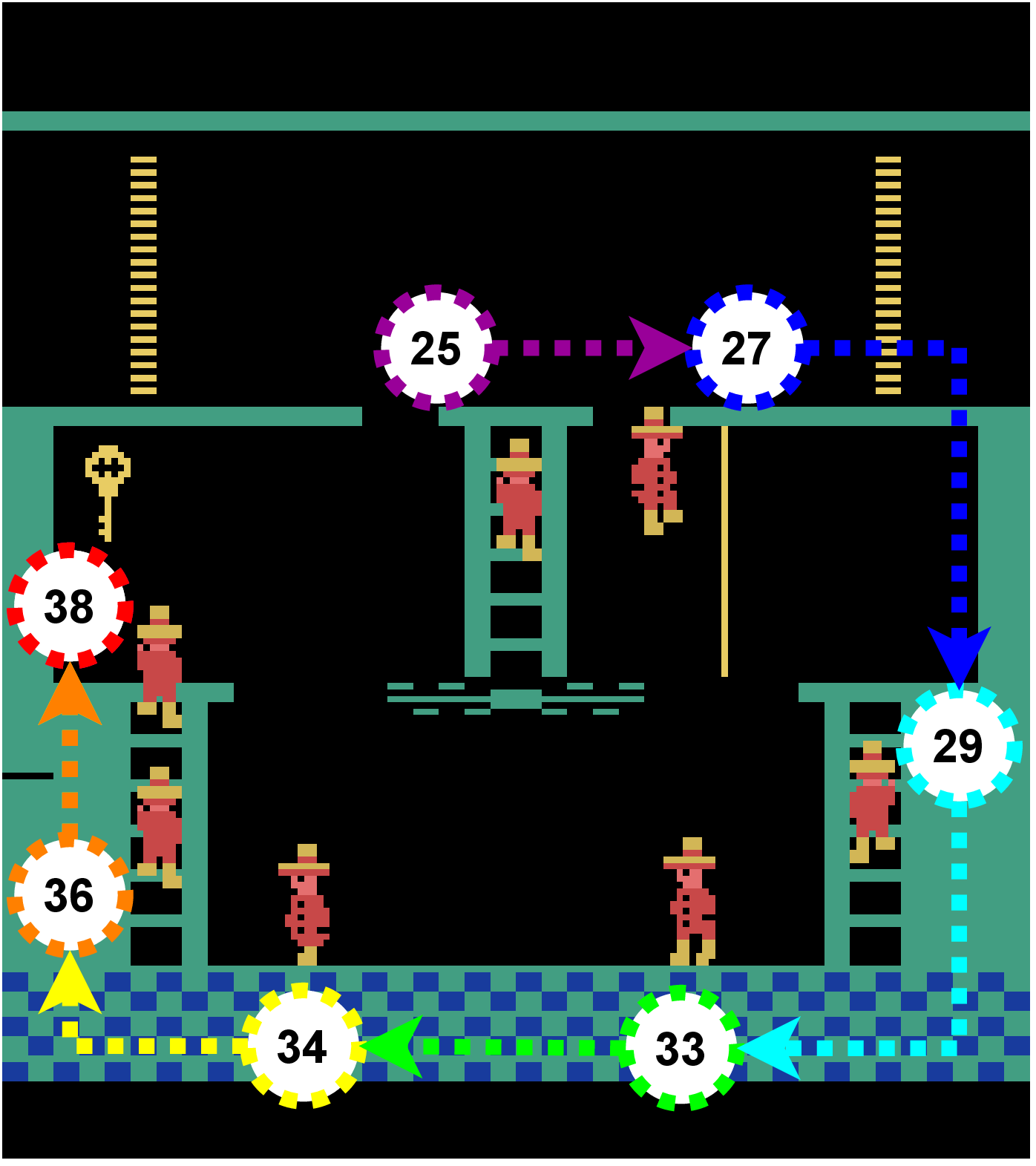
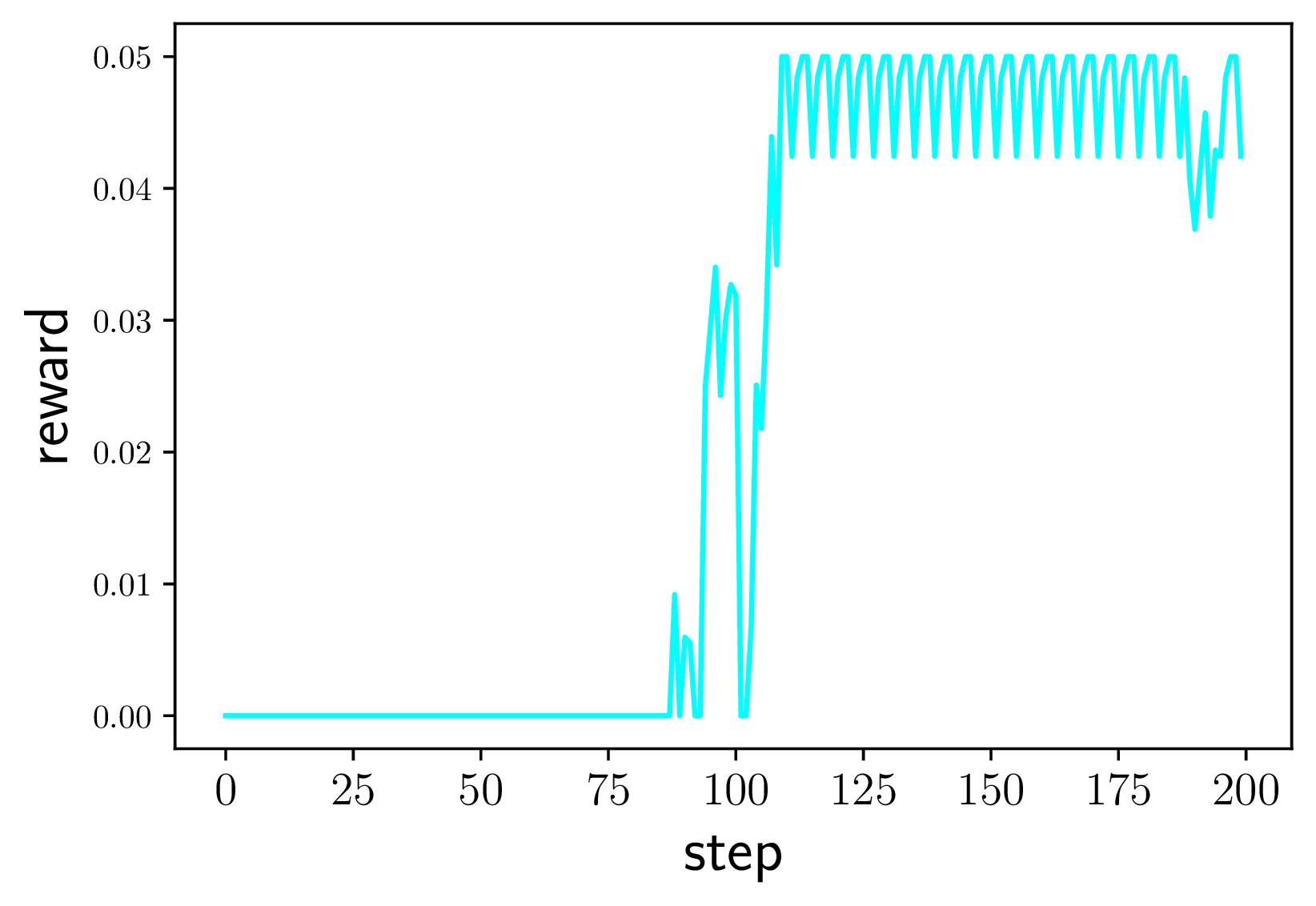
Figure 8(a) visualizes different skills. The first observations which get the maximum possible reward are overlaid. All the shown skills go to the bottom and kill the skull first. Then, they move to a specific location. It can be seen that later skills explore states further and further away from the initial state. Figure 8(b) shows that the skill receives no reward for many steps. Only after the agent has killed the skull, being on the ladder becomes rewarding ⁶ . This shows that both the reward network and the agent have learnt a lot of the concepts that are necessary to tackle Montezuma’s Revenge. This includes controlling the agent in the 2d environment, killing enemies and interacting with different objects. All of this without ever accessing the original reward function. Eventually, after solving over $200$ reward functions, the agent has the skills to visit five different rooms.

(a)	(b)	(c)

5 Conclusion

We have presented an unsupervised Reinforcement Learning algorithm that uses reward functions encoded by neural networks. Our algorithm alternates between increasing the complexity of the reward function and transferring previous knowledge to learn a new skill that finds rewarding states. This allows it to learn an unbounded number of skills that is mostly limited by the available compute power.

We have thoroughly tested the different components of our model in a 2d navigation task. This has allowed us to better understand our method in practice. We have shown that our method works both with high dimensional feature inputs, in robotic environments, and pixel inputs, in Montezuma’s Revenge. Our algorithm learned a diverse set of skills in both settings. In Humanoid and Montezuma’s Revenge, skills found by our method achieve a zero-shot performance that takes millions of steps to learn in the classical Reinforcement Learning setup.

Our approach is very general and opens up many possibilities for future research. The forward transfer mechanism can be replaced by a more complex meta-learning or off-policy relabelling techniques. Collecting data for reward function training can benefit from smarter exploration strategies. We believe our algorithm is one step in a direction that may one day allow Reinforcement Learning agents to fully understand an environment without making use of any predefined reward function. Just like in Computer Vision and Natural Language Processing, this will lead to agents that need very few labels from the task at hand to be able to solve it and will drastically expand the applicability of Reinforcement Learning.

References